Байесовский подход к предсказаниям и Маркус Гуттер

Маркус Гуттер — австралийский исследователь в области искусственного интеллекта, известный своими работами над теорией универсального ИИ и понятием универсального предсказателя. Одной из его наиболее известных концепций является AIXI — теоретическая модель, объединяющая обучение с подкреплением и байесовский подход к предсказаниям.

Основные идеи Маркуса Гуттера о предсказательной способности ИИ:

1. Универсальный предсказатель: AIXI рассматривает ИИ как алгоритм, который может максимально эффективно предсказывать будущее, основываясь на прошлых данных. Он делает это, оценивая все возможные гипотезы и выбирая наиболее вероятную.
2. Оптимальное обучение: AIXI считается теоретически оптимальной системой для обучения и принятия решений, хотя его практическая реализация слишком сложна из-за огромных вычислительных затрат.
3. Связь с Колмогоровской сложностью: Гуттер опирается на идеи Колмогоровской сложности, предполагая, что лучшее предсказание достигается с помощью наиболее сжатого описания наблюдаемых данных.
4. Ограничения и вычислительные ресурсы: Несмотря на теоретическую силу AIXI, его невозможно реализовать на практике в полном объеме из-за необходимости бесконечных вычислений. Поэтому современные системы ИИ используют приближенные методы.

Эти идеи показывают, что искусственный интеллект может предсказывать события, если он имеет доступ к достаточному количеству данных и обладает мощными алгоритмами для их анализа. Однако точность предсказаний всегда ограничена сложностью мира и доступными ресурсами.

Байесовский подход к предсказаниям — это метод, основанный на теореме Байеса, который обновляет вероятность гипотезы по мере поступления новых данных. Он широко используется в статистике, машинном обучении и искусственном интеллекте для моделирования неопределенности и принятия решений в условиях неполной информации.

Основные принципы байесовского подхода:

Теорема Байеса:

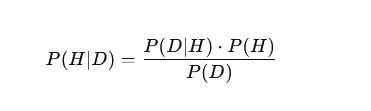
Здесь:

• P(H|D)P(H|D) — апостериорная вероятность гипотезы HH после учета данных DD,
• P(D|H)P(D|H) — вероятность наблюдения данных DD при условии, что гипотеза HH верна (правдоподобие),
• P(H)P(H) — априорная вероятность гипотезы HH до получения новых данных,
• P(D)P(D) — нормирующий множитель (общая вероятность данных).
1. Априорное и апостериорное распределение:
   • Априорное распределение (P(H)P(H)) отражает наши знания или предположения о гипотезе до получения новых данных.
   • Апостериорное распределение (P(H|D)P(H|D)) показывает, как изменяется вероятность гипотезы после учета новых данных.
2. Обновление вероятностей: Байесовский подход позволяет поэтапно уточнять предсказания, интегрируя новые данные в модель. Чем больше данных, тем точнее становится предсказание.

Применение байесовского подхода:

• Предсказание времени события (например, поломки оборудования).
• Обработка естественного языка (оценка вероятности следующего слова в тексте).
• Медицинская диагностика (оценка вероятности заболевания по симптомам).
• Финансовый анализ (предсказание рыночных изменений).

Пример:

Предположим, что существует тест на болезнь с точностью 95% (вероятность положительного результата при наличии болезни P(D|H)=0.95P(D|H) = 0.95) и с вероятностью ложноположительного результата 5% (P(D|¬H)=0.05P(D|\neg H) = 0.05). Если болезнь встречается у 1% населения (P(H)=0.01P(H) = 0.01), байесовский подход поможет рассчитать истинную вероятность наличия болезни после положительного теста:

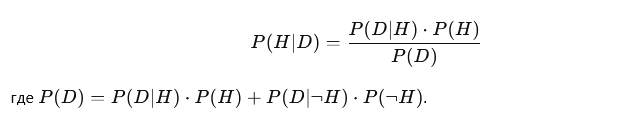
Этот подход позволяет учитывать априорные знания и адаптировать предсказания по мере поступления новых данных, что делает его мощным инструментом в ИИ.